En gestion des opérations, toutes les questions tournent en principe autour de la problématique de la maîtrise de la tâche (de la gestion des opérations). En effet, chaque gestionnaire d’une chaîne logistique est confronté en continue au choix et à l’optimisation d’un grand nombre de paramètres de gestions par rapport à un environnement, qui évolue que très rarement comme prévu. Enfin comme bien décrit par Carol Ptak et Chad Smith dans leur livre sur le DDMRP (Demand Driven Material Requirements Planning), la complexité de la tâche a encore augmenté durant ces dernières décennies :
- Evolution des chaînes logistiques locales vers un réseau mondial d’entreprises et services ;
- Des durées de vie de produits de plus en plus courtes ;
- Des délais de livraison de plus en plus court sont exigés par les clients ;
- Des produits de plus en plus complexes et variés intégrant des composants micro-électroniques ;
- Une pression de plus en plus élevée de minimiser les stocks ;
- Une fiabilité de prévisions de plus en plus faible ;
- Etc.
Ptak et Smith appellent cette situation « The New Normal ». Cela signifie que la gestion de chaînes logistiques actuelles est confrontée à de nouvelles contraintes et exigences qui rendent de plus en plus difficile l’application d’outils et de solutions classiques (comme le MRP).
Le grand nombre de solutions et de concepts existants pour la gestion de chaînes logistiques (ERP, Lean/Six Sigma, DDMRP, systèmes de planification avancées, Sales and Operations Planning, etc.) reflète la complexité de la problématique et montre que la solution miracle n’existe (malheureusement) pas. La discussion autour de la gestion de systèmes complexes comme des chaînes logistiques peut être encore approfondi en se basant sur une approche systémique.
Approche systémique
La théorie des systèmes apporte des réponses aux questions de savoir comment et sous quelles conditions des systèmes complexes peuvent être contrôlés et pilotés. Dans le livre de Gerald M. Weinberg sur ce sujet, le domaine d’application de modèles mathématiques est analysé en fonction de la complexité et du caractère aléatoire du système étudié. Comme montré sur la figure suivante, on peut définir ainsi les trois domaines I (systèmes simples à solutions analytiques), II (systèmes complexes et désorganisés à solutions statistiques) et III (systèmes complexes et organisés).
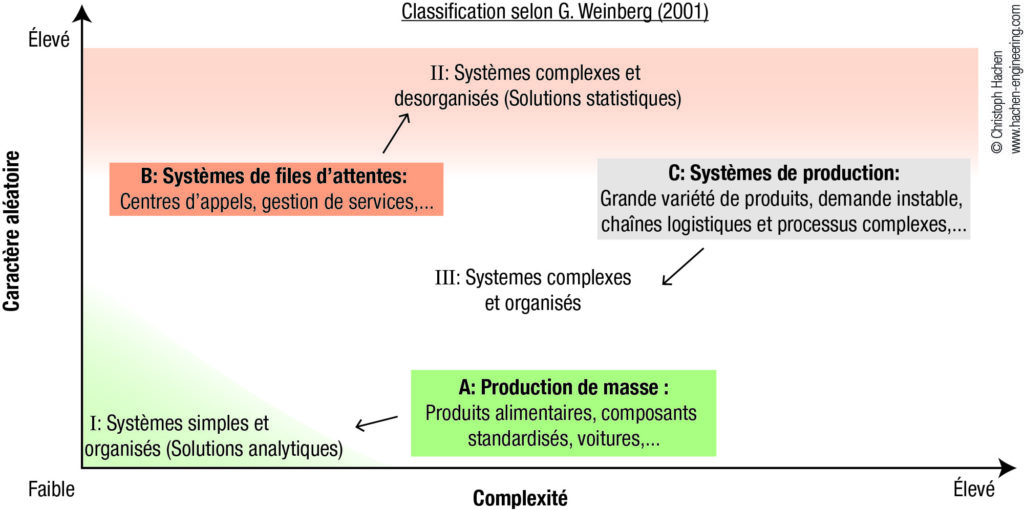
Pour des systèmes complexes et organisés, il n’existe donc pas de solutions mathématiques. Le comportement non-linéaire de systèmes ouverts comme des chaînes logistiques empêche un traitement analytique précis.
La loi de la variété requise d’Ashby confirme ce constat. Selon cette dernière, un système peut en contrôler un autre seulement si sa variété est au moins aussi élevée que celle du système contrôlé. La variété d’un système est le nombre d’états possibles d’un système, soit tous ses paramètres et caractéristiques.
La théorie des systèmes confirme donc la difficulté (ou l’impossibilité) d’obtenir des solutions mathématiques fiables pour des systèmes complexes comme des chaînes logistiques.
L’approche pragmatique
Pour tenir compte de la complexité de chaînes logistiques, l’approche pragmatique propose donc à utiliser des concepts simples pour trouver des « bonnes » solutions au lieu de chercher des solutions « optimales » en appliquant des concepts complexes. Plus en détail, cette approche est donc basée sur les idées expliquées dans les sections suivantes :
Concepts essentiels avec domaine d’application large :
Le comportement des flux de production est dicté par un certain nombre de lois simples, qui décrivent la relation entre les grandeurs logistiques comme les en-cours, les temps de passage et la performance (Hopp et Spearman, Nyhuis et Wiendahl). Ces lois sont applicables dans n’importe quel environnement de production et des actions en contradiction à leurs principes conduisent forcément à une détérioration de la performance d’un système de production. L’exemple classique est la surcharge d’un moyen de production pour assurer sa performance optimale. Une telle optimisation (locale) conduit à une détérioration globale de la performance du système, car l’augmentation des en-cours et des temps de passages rendent la gestion des opérations plus difficile (cercle vicieux de niveaux d’en-cours trop élevés). Dans l’approche pragmatique, l’application d’outils pour limiter et contrôler les en-cours est indispensable.
Spécifique :
Comme mentionné avant, LA solution miracle n’existe pas pour gérer les opérations. Cependant, beaucoup de solutions ont des domaines d’applications bien particuliers, où ils peuvent être appliqués avec succès. Un exemple typique est la méthode Kanban, qui a des propriétés très intéressantes (limitation des en-cours, éviter la surproduction, lien direct entre producteur et consommateur, etc.). Mais cette méthode n’est applicable que dans des environnements avec demande et produits « stables ». L’application de de la méthode Kanban à l’ensemble des opérations serait donc plutôt contreproductive que bénéfique.
L’approche pragmatique favorise donc des solutions mixtes ou hybrides, où plusieurs concepts sont combinés en fonction de leur domaine d’application pour obtenir un résultat global plus robuste. L’exemple classique la combinaison de la méthode Kanban (gestion des composants communs avec demande stable) avec le MRP (fabrication à la commande, produits avec une demande moins régulière) et la production répétitive (produits phares avec demande élevée et stable).
Application de stratégies de simplification/résolution de problèmes
L’application de stratégies de simplification de problèmes est indispensable dans le domaine de la gestion des opérations. Comme exemple, au lieu d’optimiser les paramètres de gestion de chaque article, on définit plutôt des règles de gestion pour des classes de produits, qui sont définis par le volume et la régularité de la demande (classification ABC-XYZ, cycle de vie des produits).
Une autre méthode essentielle est la planification hiérarchique, qui peut être comparé à la stratégie « diviser pour régner » utilisée en informatique. Le but est de diviser un problème initialement très complexe en des sous-domaines plus simples à gérer. La planification est donc divisée en une planification à long (unité de temp = mois, familles de produits finis), moyen (unité de temps = semaines, produits finis) et court (unité de temps = jours, produits et composants) terme. En général, la planification à long terme correspond au Sales and Operations Planning Process S&OP.
Ressources limitées :
Un autre avantage de l’approche pragmatique est que des solutions peuvent être trouvés avec peu d’investissements. Certes, des solutions comme la méthode Lean est confirmée par un grand nombre de « success stories », mais il est aussi certain que de telles transformations demandent des investissements très élevés en temps et en argent.
Un exemple typique est le management visuel d’ateliers de production. Des solutions comme des MES (Manufacturing Execution System) intégrées dans les ERP permettent d’afficher en temps réel l’état actuel des opérations. Ces solutions peuvent être des opportunités très intéressantes, mais elles demandent un niveau de précision très élevée au niveau des données de gestions. L’approche pragmatique favorise donc plutôt la mise en place de panneaux de planification visuelles, qui permettent une gestion simple d’ateliers, et qui peuvent être mis en place rapidement pour une fraction des investissements pour un MES.
Résumé
L’approche pragmatique propose de maîtriser la complexité (grandissante) des chaînes logistiques actuelles par l’application de méthodes simples, qui garantissent de « bonnes » solutions même dans des conditions difficiles.
Références
- Ptak C. et C. Smith. 2019. Demand Driven Material Requirements Planning (DDMPR), Version 3. Industrial Press, Inc. (en anglais)
- Weinberg, G. 2001. An introduction to General Systems Thingking. Weinberg & Weinberg (en anglais)
- Hopp W.J. et M.L. Spearman. 2000. Factory Physics : Foundations of manufacturing management, 2end edition. McGraw-Hill, New York (en anglais)
- Nyhuis, P. et H.-P. Wiendahl. 1999. Logistische Kennlinien. Springer-Verlag, Berlin Heidelberg (en allemand)